邂逅。

さて、また随分と間が空いてしまいました！

上野千鶴子氏に物申す（その２＆３＆４＆５＆6＆7＆8＆９＆１０＆１１＆１２＆・・・）とか日本のアカデミアのことことか、私的ベジタリアン観とかあとはイスラエルに行ったことで宗教観ががらっと変わりましたとか（言っておいた方が良いと思うので言いますけれど今の僕はもう anti-religion ではないです）、あとは足裏のウイルス性イボの治療がマジで痛いですとか、土曜日に城西大学で５時間講演をしましたとか今度の金曜日には筑波大でセミナー talk をしますとか今月末には慶応に行ってきますとか、書かなくてはいけないことはたくさんあるのですが、どーも今は気が向かないのでそういうことはまたそのうちに書くとして、代わりに、ここ２週間ほどの間に人生で初めて天才だと思う人に出会ったので、今日はちょっとそれについて。


彼女のお母さんにサルサで出会ったのが始まりです。

「ちょっとうちの娘の勉強を見てやってよ」と言われたので、5月の頭ぐらいからでしたか、ご飯をご馳走してもらう代わりに週に一回ご自宅にお邪魔して数学の勉強に付き合ってます。

サイン、コサインとか全然分かっていなくて、初めの３回ぐらいは

「全然勉強の出来ない子だなー」

ぐらいにしか思っていませんでした。


あれ？と思ったのは２週間ほど前です。

僕の目の前で、３次方程式をぱっと因数分解したり、3次式を１次式で割ったときの余りを一瞬で求めたりしたんですね。

もちろん、それぐらいなら（暗算のとことん苦手な）僕にでもちょっと時間をかければまあ出来ることだし、特にものすごく驚くようなことではないんですが、先週に信じられないことが起こりました。


彼女、６桁の素数を言い当てることが出来るんです！！！

なんでも、数が螺旋状に見えていて、素数には「規則」があってだから「なんとなく」見つけることが出来る、とか言うんですよね！！！


僕は驚愕して、４桁目の数字と２桁目の数字をそれぞれ１と３と指定した状態で５桁の素数を見つけることが出来るか、と聞いたら、彼女は5分ほど瞑想して、

「５桁が１の数なら多分これで全部だと思う」

と言って、１０個の数を書き上げたんです！！！

そのあと調べてみたら、その１０個の数は本当に全部素数だったんですよ！！！

信じられないですよね！！？？

さらに、この間彼女に連分数展開を教えてあげたら

「こんなのを考えたんだけれど」

と言って翌日こんな式を貰ったんです：

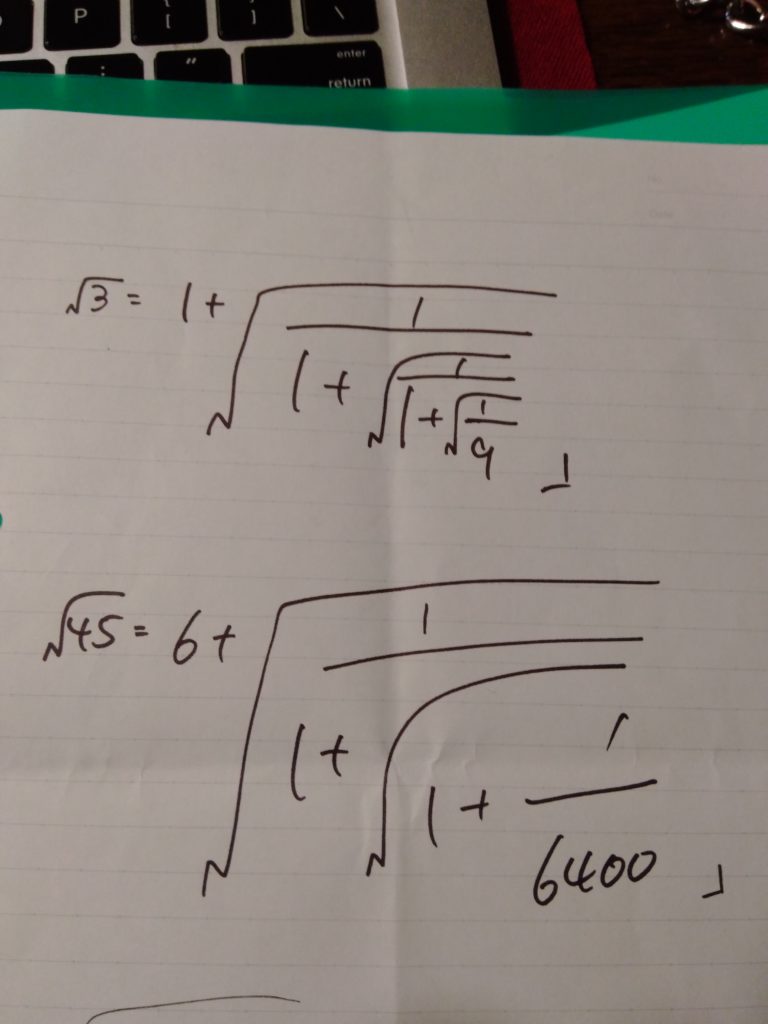
「色々やってみたけれど３と４５以外は綺麗じゃなかった」

そうです！

「何となく正しいと思う」

とか言うんです！！！

検算すら出来ないのにですよ！？信じられないですよね！！？？

（ちなみに、あとで僕が確認したら１つ目の式は等式で２つ目の式は近似式でした。）


アスペルガーや自閉症の人の中には天才的な才を持つ人がいる、なんてことはもちろん音には聞いていましたが（サヴァンの双子の話は有名ですよね）、それを遥かに上回る正真正銘の天才をここ仙台で見つけたのかも知れません。

（ちなみに学校の先生には今まで誰にも理解されなかったそうです。図形などは全然出来ないし、因数分解なども答えをパッと書いてしまうからカンニングしたんだろうと言われたりしているそうです。）



・・・さて、では今日はこの辺で失礼します！

追記（7月５日）：

彼女の才をどう育てれば良いのか思案中です。今は、とりあえず知り合いの先生達に彼女のことを話しています。何か良い考えなどがあれば僕の方までご連絡ください。